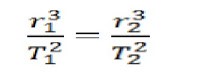Gravitasi Universal

semoga dapat bermanfaat...

TUGAS ILMU PENGETAHUAN BUMI DAN ANTARIKSA

GRAVITASI UNIVERSAL

Oleh:

Kelompok 11

Nama kelompok:

                        NI WAYAN ALFARI                                   (A 241 15 045)

                        KADEK HERI                                   (A 241 15 100)

Kelas C

Mata Kuliah:

PENGETAHUAN BUMI DAN ANTARIKSA

PROGRAM STUDI PENDIDIKAN FISIKA

FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS TADULAKO

2017

Kata Pengantar

            Puji Syukur penyusun panjatkan kehadirat Tuhan Yang Maha Esa atas segala limpahan rahmat dan karunia-Nya sehingga Makalah ini dapat diselesaikan tepat pada waktunya. Makalah ini merupakan salah satu tugas dari mata kuliah Pengetahuan Bumi dan Antariksa. Adapun judul dari makalah ini yaitu ”GRAVITASI UNIVERSAL”. Pada kesempatan ini penulis sampaikan terimakasih kepada yang terhormat Dosen  pengampuh  matakuliah.

            Penulis sadar dalam penyusunan Makalah ini masih banyak terdapat kekurangan, oleh sebab itu penulis mengharapkan saran yang membangun agar dapat menjadi acuan dalam penyusunan makalah yang akan datang. Semoga makalah ini dapat memberikan wawasan yang lebih luas kepada pembaca. Walaupun makalah ini memiliki kelebihan dan kekurangan. 

                                                                                    Palu, 15 Februari  2017

                                                                                                 Penyusun

                                                                                              Kelompok 11

Daftar Isi

Halaman Judul....................................................................................................... i

Kata Pengantar...................................................................................................... ii

Daftar Isi............................................................................................................... iii

Bab 1 Pendahuluan............................................................................................... 1

1.1. Latar Belakang............................................................................................... 1

1.2. Rumusan Masalah.......................................................................................... 1

1.3. Tujuan............................................................................................................. 1

1.4. Manfaat.......................................................................................................... 2

Bab 2 Pembahasan................................................................................................ 3

2.1. Hukum Newton Tentang Gravitasi Universal................................................ 3

2.2. Hukum Kepler................................................................................................ 6

            2.3. Implementasi Hukum Gravitasi Newton........................................................ 12

Bab 3 Penutup....................................................................................................... 15

3.1. Kesimpulan..................................................................................................... 15

3.2. Saran............................................................................................................... 15

Daftar Pustaka....................................................................................................... 16

Bab 1

Pendahuluan

1.1. Latar Belakang

            Dalam Fisika, gaya yang berperan penting menjaga keteraturan gerak planet-planet dan interaksi antarbenda ini disebut gaya gravitasi. Gravitasi adalah gaya tarik-menarik yang terjadi antara semua partikel yang mempunyai massa di alam semesta. Gravitasi matahari mengakibatkan benda-benda langit berada pada orbit masing-masing dalam mengitari matahari.

            Fisika modern mendeskripsikan gravitasi menggunakan Teori Relativitas Umum dari Einstein, namun hukum gravitasi universal Newton yang lebih sederhana merupakan hampiran yang cukup akurat dalam kebanyakankasus. Gaya gravitasi ini sangat sulit diamati, jika massa objek pengamatannya jauh lebih kecil daripada massa planet-planet. Akibatnya, Anda akan sangat sulit mengetahui berapa besar gaya gravitasi yang terjadi antara Anda dan benda-benda di sekitar Anda. Namun, Anda akan dapat dengan mudah menentukan besar gaya gravitasi yang tercipta antara Bumi dan Bulan.

1.2. Rumusan Masalah

            Dalam penulisan makalah ini, beberapa masalah yang akan dibahas yaitu sebagai berikut :

1.      Apa yang di maksud dengan Hukum Kepler dan Hukum Newton?

2.      Bagaimana Tafsiran Hukum Newton terhadap Hukum Kepler?

1.3. Tujuan

            Berdasarkan rumusan masalah diatas maka tujuan yang hendak dicapai dalam penulisan makalah ini adalah sebagai berikut :

1.      Untuk mengetahui apa yang di maksud dengan Hukum Kipler dan Hukum Newton.

2.      Untuk mengetahui bagaimana tafsiran Hukum Newton terhadap Hukum Kipler.

1.4. Manfaat

Adapun manfaat yang dapat diperolah dalam penulisan  makalah ini, yakni:

1.      Dapat di jadikan sebagai bahan pedoman untuk mengetahui apa itu Hukum Kipler dan Hukum Newton.

2.      Dapat di jadikan sebagai pedoman untuk mengetahui bagaimana tafsiran Hukum Newton terhadap Hukum Kipler.

             

Bab 2

Pembahasan

2.1. Hukum Newton Tentang Gravitasi Universal

Hukum gravitasi universal Newton menyatakan bahwa benda di alam semesta saling tarik menarik dengan gaya yang berbanding lurus dengan hasil dari massa dan berbanding terbalik dengan kuadrat dari jarak antara mereka. (Secara terpisah menunjukkan bahwa besar massa berbentuk bulat simetris tarik-menarik seolah-olah semua massa terkonsentrasi di pusat-pusat mereka.) Ini merupakan hukum fisika umum yang berasal dari pengamatan empiris yang Isaac Newton sebut induksi.

            Gejala munculnya interaksi yang berupa gaya tarik-menarik antarbenda yang ada di alam ini disebut gaya gravitasi. Setiap benda di alam ini mengalami gaya gravitasi. Jika Anda sedang duduk di kursi, sedang berjalan, atau sedang melakukan kegiatan apapun, terdapat gaya gravitasi yang bekerja pada Anda. Gaya gravitasi merupakan gaya interaksi antar benda. Di alam semesta, gaya gravitasi menyebabkan planet-planet, satelit-satelit, dan benda-benda langit lainnya bergerak mengelilingi Matahari dalam sistem tata surya dalam lintasan yang tetap.

            Isaac Newton adalah orang pertama yang mengemukakan gagasan tentang adanya gaya gravitasi. Menurut cerita, gagasan tentang gaya gravitasi ini diawali dari pengamatan Newton pada peristiwa jatuhnya buah apel dari pohonnya. Kemudian, melalui penelitian lebih lanjut mengenai gerak jatuhnya benda-benda, ia menyimpulkan bahwa apel dan setiap benda jatuh karena tarikan Bumi.

Menurut Newton, gaya gravitasi antara dua benda merupakan gaya tarik-menarik yang berbanding lurus dengan massa setiap benda dan berbanding terbalik dengan kuadrat jarak antara benda tersebut. Secara matematis, pernyataan mengenai gaya gravitasi tersebut dituliskan sebagai berikut.

dimana :

F adalah gaya antara massa,

G adalah konstanta gravitasi,

m₁ adalah massa benda pertama,

m₂ adalah massa benda kedua, dan

r adalah jarak antar pusat dari benda.

            Gaya gravitasi juga berlangsung antara matahari dan planet. Matahari yang massanya sangat besar selalu berusaha menarik planet-planet ke arahnya. Akan tetapi, planet juga berusaha mempertahankan geraknya yang cenderung lurus. Kombinasi gaya gravitasi dan  gerak planet yang cenderung bergerak lurus menyebabkan planet senantiasa beredar mengelilingi matahari.

·         Hukum Newton Pertama: setiap benda akan memiliki kecepatan yang konstan kecuali ada gaya yang resultannya tidak nol bekerja pada benda tersebut. Berarti jika resultan gaya nol, maka pusat massa dari suatu benda tetap diam, atau bergerak dengan kecepatan konstan (tidak mengalami percepatan).

·         Hukum Newton Kedua: sebuah benda dengan massa M mengalami gaya resultan sebesar F akan mengalami percepatan a yang arahnya sama dengan arah gaya, dan besarnya berbanding lurus terhadap F dan berbanding terbalik terhadap M. atau F=Ma. Bisa juga diartikan resultan gaya yang bekerja pada suatu benda sama dengan turunan dari momentum linear benda tersebut terhadap waktu.

·         Hukum Newton Ketiga: gaya aksi dan reaksi dari dua benda memiliki besar yang sama, dengan arah terbalik, dan segaris. Artinya jika ada benda A yang memberi gaya sebesar F pada benda B, maka benda B akan memberi gaya sebesar –F kepada benda A. F dan –F memiliki besar yang sama namun arahnya berbeda. Hukum ini juga terkenal sebagai hukum aksi-reaksi, dengan F disebut sebagai aksi dan –F adalah reaksinya.

2.2. Hukum Kepler

Hukum Kepler ditemukan oleh seorang matematikawan yang juga merupakan seorang astronom Jerman yang bernama Johannes Kepler (1571-1630). Penemuannya didasari oleh data yang diamati oleh Tycho Brahe (1546-1601),  seorang astronom terkenal dari Denmark.  

Sebelum ditemukannya hukum ini, manusia zaman dulu menganut paham geosentris, yaitu  sebuah paham yang membenarkan bahwa bumi merupakan pusat alam semesta. Anggapan ini didasari pada pengalaman indrawi manusia yang terbatas, yang setiap hari mengamati matahari, bulan dan bintang bergerak, sedangkan bumu dirasakan diam. Anggapan ini dikembangkan oleh astronom Yunani Claudius Ptolemeus (100-170 M) dan bertahan hingga 1400 tahun. Menurutnya, bumi berada di pusat tata surya. Matahari dan planet-planet mengelilingi bumi dalam lintasan melingkar.

Kemudian pada tahun 1543, seorang astronom Polandia bernama Nicolaus Copernicus (1473-1543) mencetuskan model heliosentris. Heliosentris artinya bumi beserta planet-planet lainnya mengelilingi matahari dalam lintasan yang melingkar. Tentu saja pendapat ini lebih baik dibanding pendapat sebelumnya. Namun, ada yang masih kurang dari pendapat Copernicus yaitu diam masih menggunakan lingkaran sebagai bentuk lintasan gerak planet.

Hukum Kepler dibagi menjadi tiga bagian, yaitu :

·         Hukum Kepler 1

     Hukum Kepler yang pertama berbunyi :

     “Setiap planet bergerak dalam lintasan elips dan matahari berada disalah satufokusnya”

     Pada waktu itu pernyataan ini dianggap radikal, karena kepercayaan yang berlaku pada saat itu memandang bahwa orbit harus didasari dengan lingkaran sempurna. Pengamatan ini sangat penting pada saat itu karena mendukung pandangan alam semesta menurut Kopernikus. Ini tidak berarti ia kehilangan relevansi dalam konteks yang lebih modern.

     Pada saat itu Kepler sendiri tidak mengetahui alasan mengapa planet bergerak dengan cara demikian. Ketika mulai tertarik dengan gerak planet-planet, Newton menemukan bahwa ternyata hukum-hukum Kepler ini bisa diturunkan secara matematis dari hukum gravitasi universal dan hukum gerak Newton. Newton juga menunjukkan bahwa di antara kemungkinan yang masuk akal mengenai hukum gravitasi, hanya satu yang berbanding terbalik dengan kuadrat jarak yang konsisten dengan Hukum Kepler.

Dimensi paling panjang pada orbit elips diatas disebut sumbu mayor alias sumbu utama, dengan setengah panjang a. Setengah panjang ini disebut sumbu semiutama alias semimayor. F₁ dan F₂ adalah titik Fokus. Matahari berada pada F₁ dan planet berada pada P. Tidak ada benda langit lainnya pada F₂. Total jarak dari F₁ ke P dan F₂ ke P sama untuk semua titik dalam kurva elips. Jarak pusat elips (O) dan titik fokus (F₁ dan F₂) adalah ea, di mana e merupakan angka tak berdimensi yang besarnya berkisar antara 0 sampai 1, disebut juga eksentrisitas. Jika e = 0 maka elips berubah menjadi lingkaran. Kenyataanya, orbit planet berbentuk elips alias mendekati lingkaran. Dengan demikian besar eksentrisitas tidak pernah bernilai nol. Nilai e untuk orbit planet bumi adalah 0,017. Perihelion merupakan titik yang terdekat dengan matahari, sedangkan titik terjauh adalah aphelion.

·         Hukum Kepler 2

     Hukum Kepler kedua ini berbunyi :

      “Luas daerah yang disapu oleh garis antara matahari dengan planet adalah sama untuk setiap periode waktu yang sama”.

     Pada selang waktu yang sangat kecil, garis yang menghubungkan antara matahari dengan planet melewati sudut (misal : dθ ). Garis tersebut melewati daerah sapuan yang berjarak r, dan luas daerah sapuan dA=1/2 r² dθ . Sementara laju planet ketika melewati daerah itu adalah dA/dt. disebut kecepatan sektor.

^{dA/dt =  1/2}r² dθ /dt

     Hal yang paling utama dalam Hukum II Kepler adalah kecepatan sektor mempunyai harga yang sama pada semua titik sepanjang orbit yang berbentuk elips. Ketika planet berada di perihelion, nilai r kecil, sedangkan dθ/dt besar. Ketika planet berada di aphelion, nilai r besar, sedangkan dθ/dt kecil. 

·         Hukum Kepler 3

     Planet yang terletak jauh dari matahari memiliki perioda orbit yang lebih panjang dari planet yang dekat letaknya. Hukum Kepler ketiga menjabarkan hal tersebut secara kuantitatif.

     “Kuadrat waktu yang diperlukan oleh planet untuk menyelesaikan satu kali orbit sebanding dengan pangkat tiga jarak rata‐rata planet‐planet tersebut dari matahari”.

     Jika T₁ dan T₂ mewakili periode dua buah planet berbeda, dan r₁dan r₂ mewakili jari-jari semimayor antara dua planet tersebut, maka dapat ditulis sebagai persamaan :

Dengan kata lain persamaan diatas dapat ditulis kembali sebagai persamaan baru sebagai berikut :

Menurut pendapat Isaac Newton, Hukum Kepler 3 dapat diturunkan secara matematis dan da[at dihubungkan dengan Hukum Newton mengenai Gaya Gravitasi Universal dan pergerakan sentripetal. Dari rumus awal hukum Kepler 3

Apabila ditinjau dengan hukum Newton kedua dan hukum gerak melingkar, maka dapat dituliskan dalam persamaan berikut :

   δF = ma ….. Persamaan hukum Newton II

    Frad = m arad   …...Persamaan Gerak melingkar

    dengan arad adalah percepatan sentripetal = /r

     Apabila ditinjau dengan hukum Newton kedua dan hukum gerak melingkar, maka dapat dituliskan dalam persamaan berikut :

      Sehingga jika diturunkan dengan pendekatan Hukum Newton II akan menjadi persamaan sebagai berikut : 

m₁ adalah massa planet pertama (akan dibandingkan dengan planet kedua) , m­_M adalah massa matahari. r ₁ adalah jari-jari rata-rata planet terhadap matahari, sedangkan v₁ adalah kelajuan orbit rata-rata planet pertama.  Waktu yang diperlukan sebuah planet untuk menyelesaikan satu orbit adalah T₁, di mana jarak tempuhnya sama dengan keliling lingkaran ( 2πr₁ ) . Dengan demikian, besar v₁ adalah :

 

Apabila metode yang sama dilakukan untuk planet kedua dengan jari-jari dan massa yang berbeda maka akan didapat persamaan umum yang sama. Dengan r₂ , m₂, T₂ berturut-turut adalah jari-jari rata-rata planet dengan matahari, massa planet dan periode orbit planet.

Perhatikan ruas kanan pada persamaan 1 dan persamaan 2, nilai antara ruas kanan persamaan 1 dan 2 adalah sama. oleh karena itu, maka apabila persamaan 1 dan 2 digabungkan maka akan menjadi persamaan hukum Kepler 3. 

Hukum Kepler 3 relevan dengan konsep gerak melingkar dan gaya gravitasi universal hasil temuan Isaac Newton dan dapat dibuktikan secara matematis.

            2.3. Implementasi Hukum Gravitasi Newton

Bagaimana para ilmuwan bisa mengetahui tentang jari-jari bumi ataupun massa bumi. alat ukur apa yang digunakan. Masih kelanjutan tentang gaya gravitasi yang menjadi dasar keilmuwan kita sebelumnya, para ilmuwan bisa memecahkan persoalan tersebut yang mungkin pernah ada dalam benak kita

Berdasarkan hukum gravitasi Newton, data-data tersebut digunakan untuk menghitung besaran lain tentang benda ruang angkasa yang tidak mungkin diukur dalam laboratorium.

      1.      Menghitung Massa Bumi

Massa bumi dapat dihitung dengan menggunakan nilai G yang telah diperoleh dari percobaan Cavendish. Anggap massa bumi M dan jari-jari bumi R = 6,37 × 106 m (bumi dianggap bulat sempurna). Berdasarkan rumus percepatan gravitasi bumi, Anda bisa menghitung besarnya massa bumi.

      2.      Menghitung Massa Matahari

Telah Anda ketahui bahwa jari-jari rata-rata orbit bumi rB = 1,5 × 1011 m
dan periode bumi dalam mengelilingi matahari TB = 1 tahun = 3 × 107 s.
Berdasarkan kedua hal tersebut serta dengan menyamakan gaya matahari
dan gaya sentripetal bumi, maka dapat diperkirakan massa matahari.

      3.      Menghitung Kecepatan Satelit

Suatu benda yang bergerak mengelilingi benda lain yang bermassa lebih besar dinamakan satelit, misalnya bulan adalah satelit bumi. Sekarang banyak satelit buatan diluncurkan untuk keperluan komunikasi, militer, dan riset teknologi. Untuk menghitung kecepatan satelit dapat digunakan dua cara, yaitu hukum gravitasi dan gaya sentrifugal.

a)      Menghitung Kecepatan Satelit Menggunakan Hukum Gravitasi

                 Anggap suatu satelit bermassa m bergerak melingkar mengelilingi    bumi pada ketinggian h dari permukaan bumi. Massa bumi M dan jari-jari             bumi R. Anda tinjau gerakan satelit dari pengamat di bumi. Di sini gaya     yang bekerja pada satelit adalah gaya gravitasi. Berdasarkan rumus hukum II  Newton,  Anda dapat mengetahui kecepatan satelit

b)      Menghitung Kecepatan Satelit Menggunakan Gaya Sentrifugal
            Sebuah satelit memiliki orbit melingkar, sehingga dalam acuan ini, satelit akan merasakan gaya sentrifugal (mv2/r2). Gaya sentrifugal muncul karena pengamatan dilakukan dalam sistem non inersial (sistem yang dipercepat, yaitu satelit). Gaya sentrifugal besarnya sama dengan gaya gravitasi.

      4.      Menghitung Jarak Orbit Satelit Bumi

Apabila satelit berada pada jarak r dari pusat bumi, maka kelajuan satelit saat mengorbit bumi dapat dihitung dengan menyamakan gaya gravitasi satelit dan gayasentripentalnya. 

Bab 3

Penutup

3.1. Kesimpulan

            Hukum gravitasi universal Newton menyatakan bahwa benda di alam semesta saling tarik menarik dengan gaya yang berbanding lurus dengan hasil dari massa dan berbanding terbalik dengan kuadrat dari jarak antara mereka.

Kepler mengemukakan bahwa planet bergerak dengan kelajuan tidak konstan tetapi bergerak lebih cepat ketika dekat dengan matahari dibanding saat jauh dengan matahari. Hukum Kepler di bagi atas 3 bagian yaitu Hukum I Kepler menyatakan bahwa semua planet bergerak dalam orbit elips dengan matahari sebagai salah satu fokusnya. Hukum II Kepler menyatakan bahwa garis yang menghubungkan tiap planet ke matahari menyapu luasan yang sama dalam waktu yang sama. Pada hukum III Kepler menyatakan bahwa kuadrat periode tiap planet sebanding dengan pangkat tiga jarak rata-rata planet dari matahari.

3.2. Saran

            Makalah ini dapat dijadikan sebagai dasar untuk untuk memahami pengetahuan bumi dan antariksa khususnya tentang materi gravitasi universal hubungan antara hukum Newton dan Hukum Kepler.

Daftar Pustaka

Aisah, E. 2012. Hubungan Hukum Kepler dengan Hukum Newton. [Online],          Tersedia: http://eliaisah.blogspot.co.id/2012/09/hubungan-hukum-kepler-        dengan-hukum.html. [15 Februari 2017]           

Resmiyanto, R. 2011. Hukum Gravitasi Newton: Sedikit Tafsir Alam. [Online],             Tersedia:http://rachmadresmi.blogspot.co.id/2011/04/hukum-gravitasi-        newton-sedikit-tafsir.html. [15 Februari 2017]

Rusmin. 2015. Pengetahuan Bumi dan Antariksa. [Online], Tersedia:             http://rusminfisika.blogspot.co.id/2015/03/gravitasi-universal.html.

            [15 Februari 2017]